-
配列の要素が次のようになっているとき、一番左端の要素とそれより右にある要素を順番に比べて、もし右側の要素が左端の要素より小さければ交換して最終的に一番左に最小値が来るようにする。
次に左から2番目の要素とそれより右にある要素を順番に比べて最初と同じように交換する。
これを繰り返して最終的に要素を小さいもの順に並べ替えるようにしてください。(これを選択ソートといいます。退避用の変数を使ってください。)
結果の表示は以下のようにしてください。 -
整列前 [8, 3, 5, 1, 7]
整列後 [1, 3, 5, 7, 8]
選択ソート法
「選択ソート法」というのは、順に比較する先頭位置をずらしながら他の要素の値と大小を比較していって、交換するしないを繰り返すことで並び替えを行う方法です。
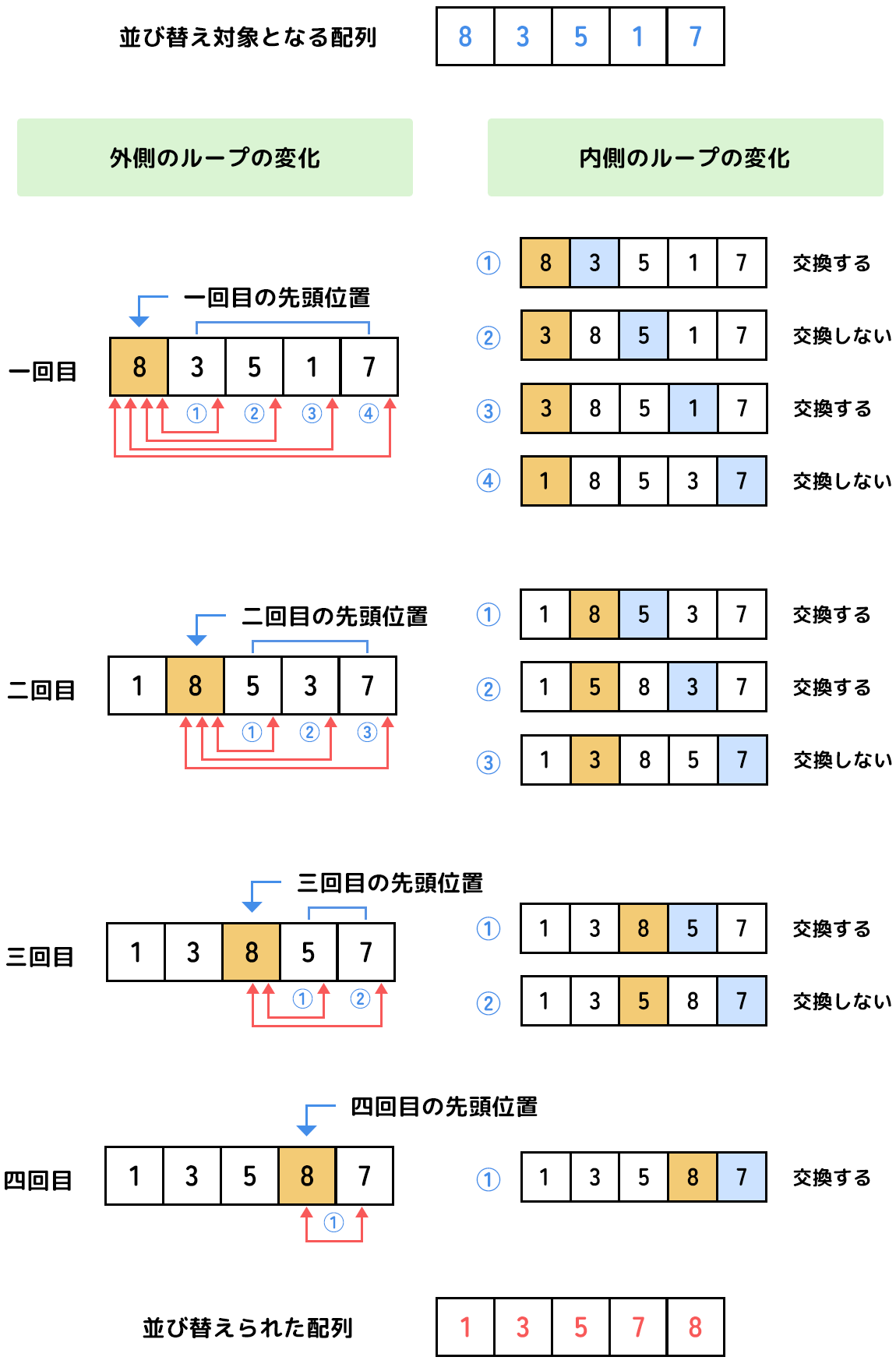

変数の交換を使うといいね。
この図の考え方を使うんだね。

📖 解答例
a = [8, 3, 5, 1, 7]
n = 5
print('整列前', a)
print()
for i in range(0, n - 1, 1):
for j in range(i + 1, n, 1):
if a[i] > a[j]:
temp = a[i]
a[i] = a[j]
a[j] = temp
print('整列後', a)
-
配列の要素が次のようになっているとき、右端から始めて隣り合う要素を順番に比べて、もし右側の要素が左側の要素より小さければ交換して最終的に一番左に最小値が来るようにしてください。
そして、同様に右端から順次比較して交換を繰り返し、左から2番目に次に小さい数が来るようにしてください。
これを繰り返して最終的に要素が小さい順に並ぶようにしてください。(これをバブルソートといいます。退避用の変数を利用してください。) -
a = [8, 3, 5, 1, 7]
表示:整列前 [8, 3, 5, 1, 7]
整列後 [1, 3, 5, 7, 8]

今回はちょっと難しいね。右端から比較するにはどうすればいいか、頑張って考えてみてね!
次の図のように考えてみよう!

バブルソート法
「バブルソート法」というのは、隣り合った要素の値と大小を比較していって、交換するしないを繰り返すことで並び替えを行う方法です。
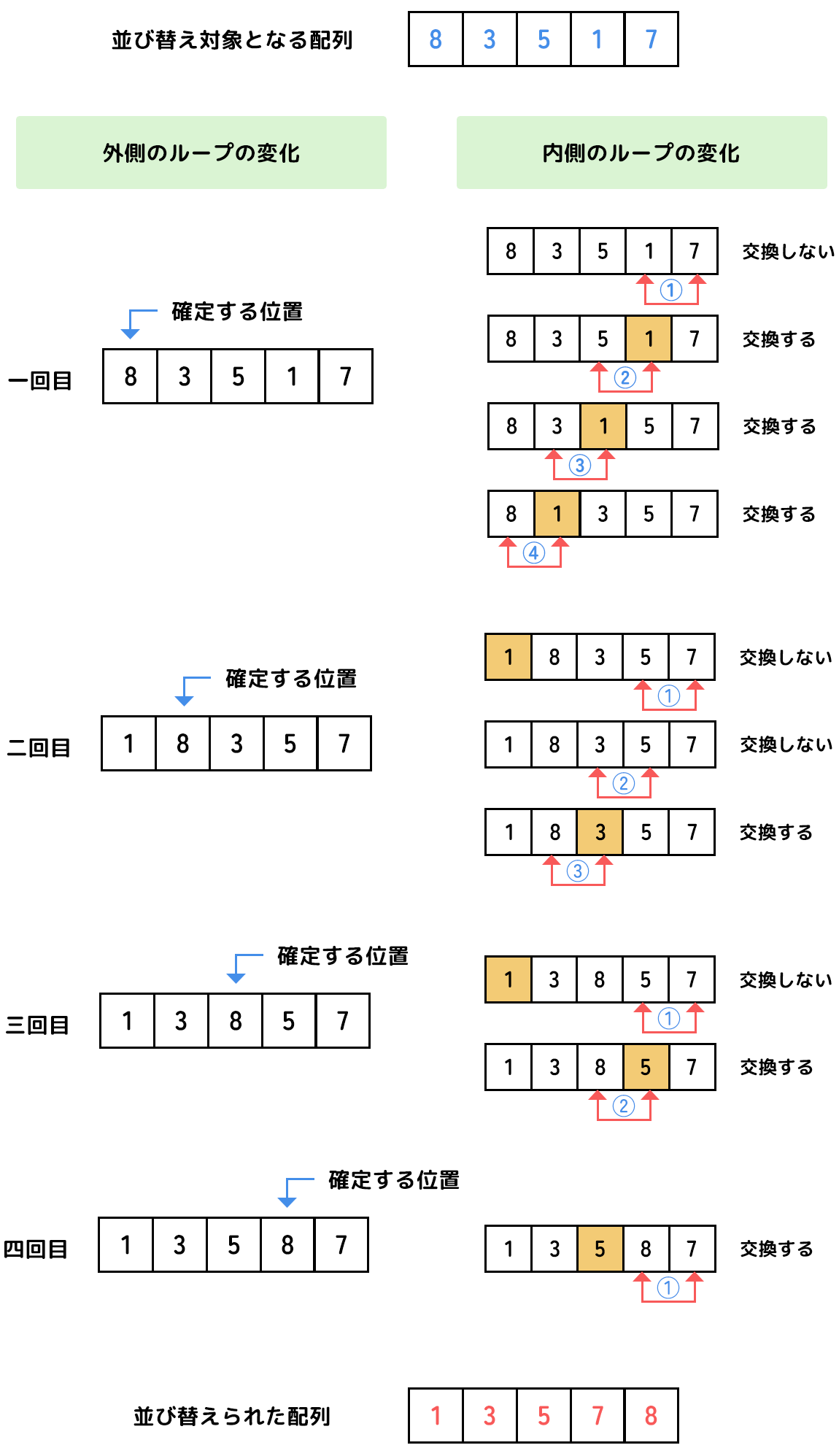
📖 解答例と解説
#バブルソート
a = [8, 3, 5, 1, 7]
n = 5
print('整列前', a)
for i in range(0, n - 1, 1):
for j in range(n - 2, i - 1, -1):
if a[j] > a[j + 1]:
temp = a[j]
a[j] = a[j + 1]
a[j + 1] = temp
print()
print('整列後', a)

確定する位置がだんだん右に動いていくね。
for文のところで少し苦労するね。i は確定する場所と考えるといいね。j は間隔が-1なので添字は順に小さくなっていくのだね。


変数交換は 変数1,変数2=変数2,変数1 を使う方法もあるね。
temp = a[j]
a[j] = a[j+1]
a[j+1] = temp
の代わりに、a[j],a[j+1] = a[j+1],a[j]としても同じ結果になるよ。
