-
税込価格計算をしてください。
商品名、値段、状況(takeoutかeatin)を入れる変数をそれぞれ作成してください。
自分で税込価格を計算する関数を作って、表示する処理と分けてください。


ドーナツ屋さんでドーナツを買うことにしよう!
その時、店員さんに店内で食べる(イートイン)か、お持ち帰り(テイクアウト)するかを聞かれるよね。


それはどちらにするかで、消費税率が変わって、合計金額も変わるからなんだよ!
状況に合わせて、消費税率を変えて計算する関数を作ればいいね!

📖 解答例と解説
def calc(price, category):
if(category == "takeout"):
ans = int(price * 1.1)
elif(category == "eatin"):
ans = int(price * 1.08)
else:
ans = "error"
return ans
name = "抹茶ドーナツ"
price = 200
category = "eatin"
ans = calc(price, category)
print(name, ":", ans, "円")

税込価格を計算する、calc関数を作ったよ!
条件分岐構造で、変数categoryの中身によって消費税率を変えて計算しているんだよ!

-
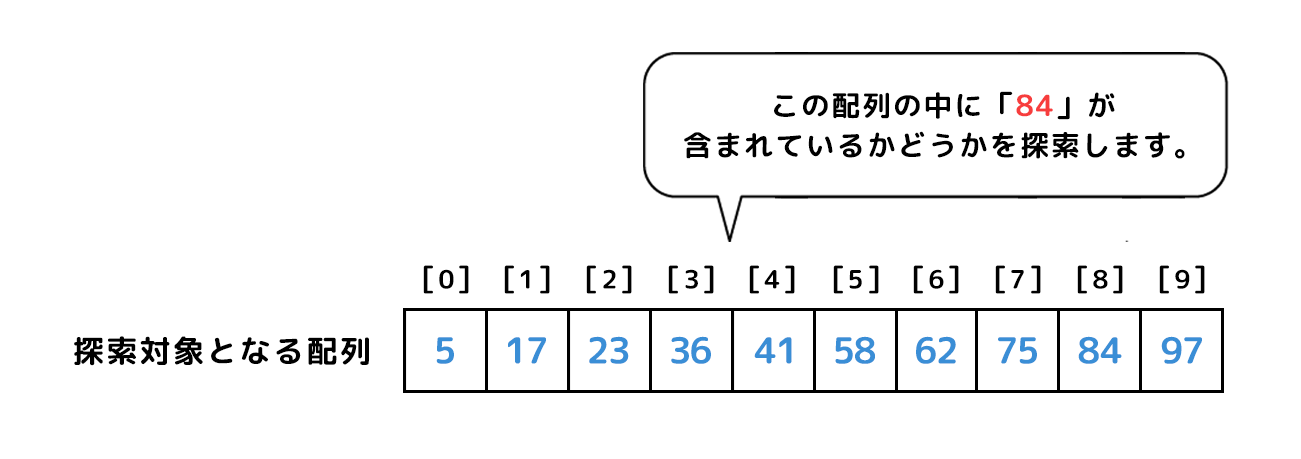
配列の中から目的の値があるかを見つけ出すことを探索といいます。
端から順に目的の探索値を探し出すことを線形探索といい、探索範囲を半分に絞り込みながら探索値を探し出すアルゴリズムを二分探索といいます。
ただし、二分探索を行うためにはデータが昇順または降順に整列している必要があります。いま、整列されていないデータが与えられた時、ソートするための関数を作り、それを呼び出してソートしたのちに二分探索を行うようにしてください。 -
与えられた配列をa=[97,58,23,75,17,5,84,41,36,62]とします。
以下のように表示してください。 -
整列前 [97, 58, 23, 75, 17, 5, 84, 41, 36, 62]
整列後 [5, 17, 23, 36, 41, 58, 62, 75, 84, 97]
探索値は 62
62 は、整列後の7番目に存在

ソートするための関数を作るときは、応用問題10のソートで勉強したアルゴリズムを使うといいね!
二分探索は順番に並んでいるデータの中から見つけたいデータを探すときに効率よく探す方法だよ!
次の図のように考えるんだね。ちょっと難しいけれどできるかな?


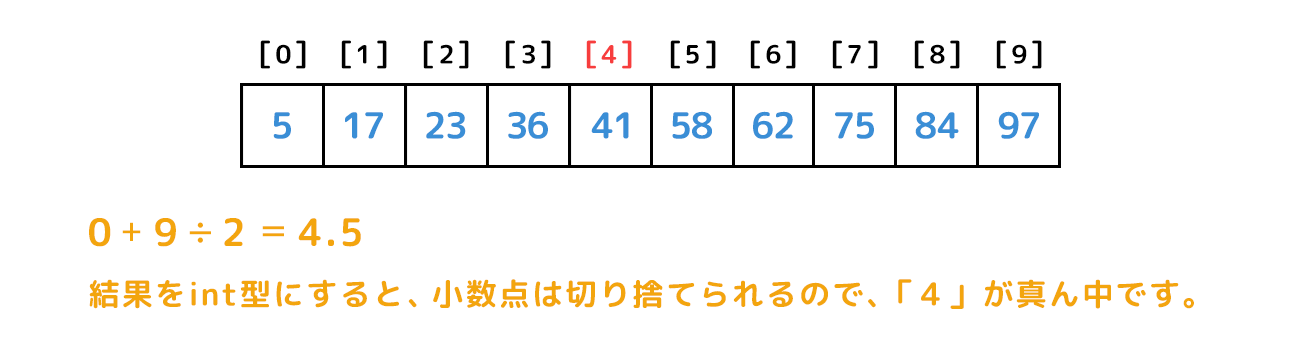
二分探索では、真ん中のデータと比較して目的の値がそれより大きいか小さいかを判断するよ!
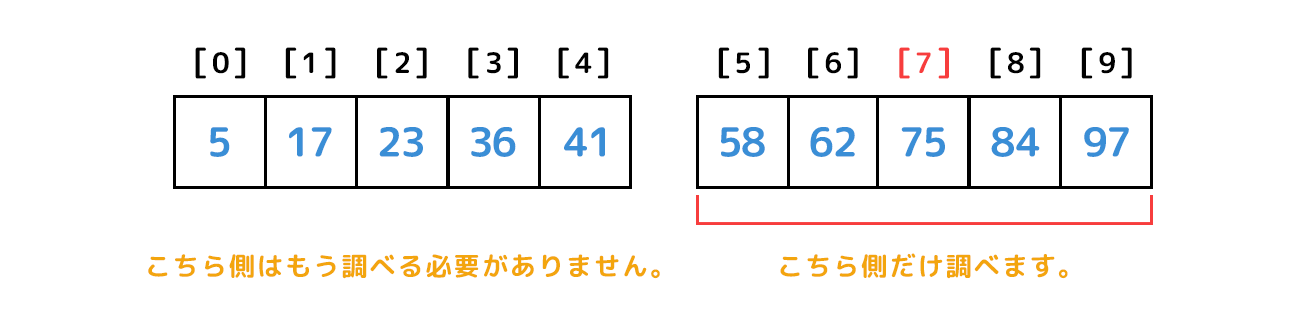
目的の値が真ん中のデータと比べて大きかったら真ん中のデータより右側に含まれるって分かるよね!


それが分かったら、含まれていないほうの半分はもう調べなくてもいいよね!
そうやって探索の範囲を半分に狭めながら確認を繰り返して、目的のデータが見つかるまで絞り込んでいくんだよ!
二分探索の考え方を確認して、問題に取り組んでみよう!

📖 解答例と解説
#選択ソートの関数定義
def seiretu(x, y):
for i in range(0, y - 1, 1):
for j in range(i + 1, y, 1):
if x[i] > x[j]:
temp = x[i]
x[i] = x[j]
x[j] = temp
print('整列後', x)
a = [97, 58, 23, 75, 17, 5, 84, 41, 36, 62]
n = len(a)
print('整列前', a)
#ソートするための関数を呼び出す
seiretu(a, n)
s = int(input())
print('探索値は', s)
#二分探索開始
left = 0; right = n - 1
while left <= right:
m = int((left + right) // 2)
if a[m] == s:
print(s, 'は、整列後の', m + 1, '番目に存在')
break
#中央値 > 探索値の場合
if a[m] > s:
right = m - 1
#中央値 < 探索値の場合
else:
left = m + 1

線形探索だと全部のデータを調べるので、データが多いと時間がかかるけれど二分探索だと、半分に絞り込むから高速に探索できるんだ。
m=(left+right)//2 は足して2で割った値の小数点以下を切り捨てる計算だよ。


中央値と探索値が一致したら break でループを抜けるんだね。
じつは、Pythonにはソート関数も準備されているんだ。
#関数呼び出し
a.sort()
print('整列後', a)
とすると呼び出して整列したものを表示できるよ。

